Unlocking The Mystery Of √16: Your Complete Guide To Square Roots
Have you ever wondered about the fundamental building blocks of mathematics, those simple concepts that underpin more complex ideas? One such foundational concept is the square root. And when it comes to illustrating this concept, few numbers offer as clear and straightforward an example as the number 16. Understanding the square root of 16 is not just about memorizing a number; it's about grasping a core mathematical operation that has widespread applications in various fields.
In this comprehensive guide, we'll embark on a journey to demystify square roots, with a particular focus on the number 16. We'll explore what a square root truly is, delve into why 16 holds a special place as a "perfect square," and walk through various methods to calculate its square root, from intuitive approaches to more systematic techniques. Beyond the basics, we'll even touch upon intriguing scenarios like the square roots of negative numbers and complex expressions, ensuring you gain a holistic understanding of this essential mathematical concept.
Table of Contents
- What Exactly is a Square Root? Defining the Core Concept
- Understanding the Square Root of 16: The Basics
- Why is 16 a "Perfect Square"? A Deeper Dive
- Diverse Methods to Calculate the Square Root of 16
- Beyond the Basics: Square Roots of Negative Numbers and Complex Expressions
- Practical Applications of Square Roots in the Real World
- Common Misconceptions and Important Notes about Square Roots
- The Enduring Significance of Square Roots in Mathematics
What Exactly is a Square Root? Defining the Core Concept
At its heart, a square root is one of the most fundamental operations in arithmetic and algebra, serving as the inverse operation to squaring a number. To "square" a number means to multiply it by itself (e.g., 5 squared is 5 × 5 = 25). Conversely, finding the square root of a number means discovering what number, when multiplied by itself, yields the original number. This concept is elegantly summarized by the statement: "The square root of a number is the inverse of squaring that number, i.e., it gives the original number when multiplied by itself." The symbol used to denote a square root is the radical symbol, written as √. So, when you see √x, you are being asked to find the square root of x. For instance, √25 asks: "What number, when multiplied by itself, equals 25?" The answer, of course, is 5, because 5 × 5 = 25. It's crucial to understand that every positive number actually has two square roots: a positive one and a negative one. For example, for the number 16, both 4 and -4 are square roots, because 4 × 4 = 16 and (-4) × (-4) = 16. However, by convention, when we use the radical symbol (√), we are typically referring to the *principal* (or positive) square root. So, √16 explicitly means the positive square root, which is 4. This distinction is vital for clarity in mathematical expressions and problem-solving.Understanding the Square Root of 16: The Basics
When we apply the definition of a square root to the number 16, the answer becomes immediately clear and demonstrative. "The square root of 16 is 4 because 42 = 16." This simple equation encapsulates the entire concept. We are looking for a number that, when multiplied by itself, results in 16. That number is unequivocally 4. This fact makes the **square root of 16** an ideal starting point for anyone learning about square roots. It's a clean, exact answer, devoid of decimals or complex fractions, which isn't always the case for other numbers. Furthermore, the number 16 possesses a unique characteristic in the world of square roots: it is a "perfect square." This means its square root is a whole number, specifically an integer. Beyond being a perfect square, the **square root of 16**, which is 4, is also classified as a rational number. A rational number is any number that can be expressed as a fraction p/q, where p and q are integers and q is not zero. Since 4 can be written as 4/1, it fits this definition perfectly. This contrasts with the square roots of non-perfect squares, like √2 or √3, which are irrational numbers and cannot be expressed as simple fractions. The simplicity and exactness of √16 make it a cornerstone example in introductory mathematics. You can also express the square root of 16 using exponential notation, as (16)1/2, further illustrating its mathematical properties.Why is 16 a "Perfect Square"? A Deeper Dive
The term "perfect square" is a crucial concept when discussing square roots. A number is deemed a perfect square if its square root is an integer (a whole number, positive or negative). In simpler terms, "A square number is formed when a number is multiplied by itself." For example, 9 is a perfect square because 3 × 3 = 9. Similarly, 25 is a perfect square because 5 × 5 = 25. The number 16 perfectly fits this definition because 4 multiplied by itself (4 × 4) equals 16. This property simplifies the process of finding its square root immensely. When you encounter a perfect square under the radical symbol, you know immediately that the result will be a clean, exact integer, without any remaining radical terms or endless decimal expansions. This is why "Finding the square root of 16 is straightforward, as 16 is a perfect square." The significance of perfect squares extends beyond just yielding neat answers. They are fundamental in various mathematical contexts, from simplifying complex radical expressions to understanding number theory. Recognizing perfect squares quickly can save time and effort in calculations. For instance, if you're simplifying an expression like √48, knowing that 16 is a perfect square and a factor of 48 (48 = 16 × 3) allows you to simplify it as √(16 × 3) = √16 × √3 = 4√3. This demonstrates how understanding perfect squares, like 16, can be applied to more complex problems, allowing you to pull out the perfect square factor from under the radical.Diverse Methods to Calculate the Square Root of 16
While the **square root of 16** is easily identifiable by inspection, understanding various methods to calculate square roots is invaluable. These methods provide a deeper insight into the mathematical process and equip you to find the square roots of more complex numbers. "Learn how to find the square root of 16 using different methods, such as guess and check, prime factorization, division, and calculator." Let's explore some of these techniques.The Guess and Check Method: An Intuitive Approach
The guess and check method, also known as trial and error, is perhaps the most intuitive way to approach finding a square root, especially for perfect squares. The process involves making an educated guess, squaring that guess, and then adjusting your next guess based on whether your squared value is too high or too low. For the **square root of 16**: 1. **Initial Guess:** Let's start with a guess, say 3. 2. **Check:** 3 × 3 = 9. This is too low (9 < 16). 3. **Adjust Guess:** We need a larger number. Let's try 5. 4. **Check:** 5 × 5 = 25. This is too high (25 > 16). 5. **Refine Guess:** Since 3 was too low and 5 was too high, the answer must be between 3 and 5. The only integer left is 4. 6. **Final Check:** 4 × 4 = 16. This is correct! This method is excellent for building number sense and understanding the concept of squaring, but it becomes less efficient for larger numbers or non-perfect squares.Prime Factorization Method: Breaking Down the Number
The prime factorization method is a systematic way to find square roots by breaking a number down into its prime factors. This method is particularly useful for perfect squares and for simplifying non-perfect squares. To find the **square root of 16** using prime factorization: 1. **Find the prime factors of 16:** * 16 ÷ 2 = 8 * 8 ÷ 2 = 4 * 4 ÷ 2 = 2 * 2 ÷ 2 = 1 So, the prime factorization of 16 is 2 × 2 × 2 × 2. 2. **Group the factors in pairs:** Since we are looking for a square root, we group identical prime factors into pairs. * (2 × 2) × (2 × 2) 3. **Take one factor from each pair:** For each pair, take one of the factors outside the square root. * From the first pair (2 × 2), take 2. * From the second pair (2 × 2), take 2. 4. **Multiply the chosen factors:** * 2 × 2 = 4. Therefore, the **square root of 16** is 4. This method is also very effective for simplifying more complex radical expressions. For instance, consider the example from the provided data: "To find the square root of 48: 48 = 16 × 3 = 42 × 3. Since 16 (or 42) is a perfect square, we can pull it out of the square root, √48 = √(16 × 3) = √16 × √3 = 4√3." This demonstrates the power of prime factorization in breaking down numbers and simplifying radicals to their simplest form.The Long Division Method: A Systematic Calculation
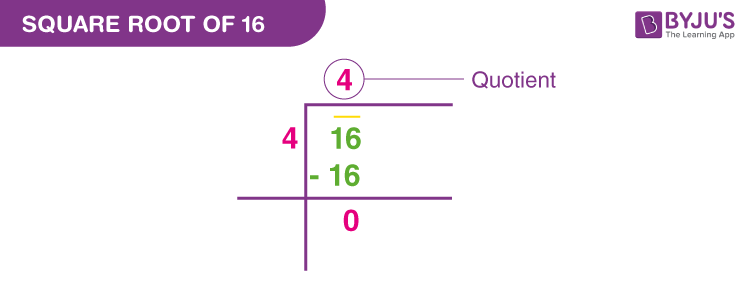
The long division method for square roots is a more complex but highly systematic algorithm that can find the square root of any number, including those that are not perfect squares, to any desired degree of precision. While it might seem overkill for a simple number like 16, understanding its principles highlights the depth of square root calculation. For the **square root of 16**: 1. **Pair the digits:** Starting from the decimal point (or the rightmost digit for integers), group the digits in pairs. For 16, it's just '16'. 2. **Find the largest digit whose square is less than or equal to the first pair:** The first (and only) pair is 16. The largest integer whose square is ≤ 16 is 4 (since 42 = 16). 3. **Write the digit:** Write 4 as the first digit of the square root. 4. **Subtract and bring down:** Subtract 42 (16) from 16, which leaves 0. Bring down the next pair (if any, in this case, there are none, or we can imagine '00' for decimals). 5. **Double the current root and add a blank:** Double the current root (4 × 2 = 8) and append a blank digit (8_). We need to find a digit to put in the blank such that (8_ × _) is less than or equal to the remainder (0). Since the remainder is 0, the digit must be 0. 6. **Final Result:** The square root is 4. This method is more commonly taught for finding the square roots of larger numbers or for calculating decimal approximations, but it rigorously confirms that the **square root of 16** is indeed 4.Leveraging Technology: Calculators and Square Root Tables
In the modern era, the most common and expedient way to find a square root is by using a calculator or computer software. Digital tools, from simple handheld calculators to advanced spreadsheet programs like Excel or Google Sheets, have built-in functions for this purpose. * **Using a Calculator:** Simply enter the number 16 and press the square root button (often marked as √ or SQRT). The display will immediately show 4. * **Using Excel or Google Sheets:** For those working with data, the `SQRT()` function is invaluable. If you type `=SQRT(16)` into any cell, it will return 4. This is a quick and efficient way to "calculate the square root of 16 in excel or google sheets." * **Square Root Tables:** Before the widespread availability of calculators, mathematicians and students relied on square root tables. These tables listed numbers and their corresponding square roots, often to several decimal places. While largely obsolete for exact calculations due to digital tools, they represent a historical method for "learn how to find the square root of 16 using... the square root table." They are still useful for quick estimations or understanding the magnitude of square roots. These technological aids make finding square roots almost instantaneous, allowing focus on applying the results rather than the calculation itself. However, understanding the underlying manual methods provides a deeper appreciation for how these tools arrive at their answers.Beyond the Basics: Square Roots of Negative Numbers and Complex Expressions
While the **square root of 16** is a straightforward real number, the concept of square roots extends into more complex mathematical territories, particularly when dealing with negative numbers or
The Square Root of 16 - YouTube

How To Find 16 Square Root: Detailed Explanation - The Story of
Square Root of 16 | How to Find the Square Root of 16?