Unlocking The Mystery Of The Less Than Sign: Your Ultimate Guide
Table of Contents:
- Introduction
- What Exactly is the Less Than Sign?
- The Fundamental Role of the Less Than Sign in Mathematics
- Teaching and Remembering the Less Than Sign: Tricks and Tips
- Beyond Basic Numbers: Applications of the Less Than Sign
- The Less Than Sign in the Digital World: Typing and Unicode
- Common Pitfalls and FAQs About the Less Than Sign
- Conclusion
Introduction
Have you ever encountered the curious < and > symbols and wondered about their true meaning and power? These seemingly simple characters, often referred to as the "less than sign" and "greater than sign," are far more than just abstract mathematical notations. They are fundamental tools that underpin our understanding of relationships between quantities, essential not only in the classroom but also in diverse fields from computer science to economics. This comprehensive guide aims to demystify the less than sign, exploring its origins, applications, and practical tips for remembering its correct usage.
From comparing the number of marbles in two bowls to evaluating complex algorithms, the less than sign (<) serves as a universally recognized shorthand for expressing that one value is smaller than another. Its ubiquity across various disciplines highlights its importance as a foundational concept. Whether you're a student struggling to grasp inequalities, a professional looking to refresh your mathematical understanding, or simply curious about the symbols that shape our numerical world, this article will provide you with the expertise and clarity you need to master the less than sign with confidence.
What Exactly is the Less Than Sign?
At its core, the less than sign (<) is a mathematical comparison symbol used to show an inequality between two values. It signifies that the value on its left side is smaller than the one on its right side. For instance, when we write "6 < 8," we are stating unequivocally that '6 is less than 8'. This simple yet profound symbol establishes a basic ordinal relationship between numbers, allowing us to compare quantities efficiently and precisely. It's a fundamental notation, universally recognized and ubiquitously used, simplifying comparisons and expressing relationships between numerical values effectively.
The less than symbol is part of a family of inequality symbols, which also includes the greater than sign (>), less than or equal to (≤), greater than or equal to (≥), and not equal to (≠). While each has its specific role, the less than sign is perhaps one of the most frequently encountered, serving as a gateway to understanding more complex mathematical expressions and logical operations. It states that one value is lesser than, lower than, fewer than, or smaller than the other, providing a clear and concise way to represent these comparisons. The less than sign and the greater than sign look like a 'v' on its side, a simple visual cue that aids in recognition. This foundational understanding is crucial for anyone engaging with numerical data, from elementary school students to advanced data scientists.
The Fundamental Role of the Less Than Sign in Mathematics
The significance of the less than sign extends far beyond simple number comparisons. It is a cornerstone of mathematical reasoning, enabling us to define ranges, express conditions, and solve problems across various branches of mathematics. Its role is pivotal in algebra, calculus, statistics, and even geometry when dealing with magnitudes and distances. Without this basic comparison symbol, many advanced mathematical concepts would be challenging, if not impossible, to articulate.
Comparing Numbers and Quantities
The most straightforward application of the less than sign is in comparing two distinct numerical values. This comparison is a foundational skill taught early in mathematics education. For example, if we have 4 marbles in bowl A and 7 marbles in bowl B, we can express this relationship using the less than symbol as "4 < 7." This visually represents that the quantity of marbles in bowl A is indeed less than the quantity in bowl B. This metric allows us to compare numbers, weights, heights, and various other values in a standardized way. The ability to quickly ascertain which value is smaller is critical for everyday tasks, from budgeting to interpreting scientific data. Consider comparing temperatures: -5°C < 0°C clearly indicates that -5 degrees Celsius is colder than 0 degrees Celsius, a critical understanding in many scientific and practical contexts. This simple comparison forms the bedrock of quantitative literacy.
Understanding Inequalities
Beyond simple comparisons, the less than sign is integral to understanding and working with inequalities. An inequality is a statement that two expressions are not equal, often indicating a range of possible values rather than a single specific value. For instance, if we say "x < 10," we are stating that 'x' can be any number less than 10, but not 10 itself. This concept is vital for:
- Defining Domains and Ranges: In functions and mathematical models, inequalities help define the set of input values (domain) for which a function is valid, or the set of output values (range) it can produce. For example, the domain of a square root function requires the input to be greater than or equal to zero, while a certain physical quantity might be constrained to be less than a maximum value.
- Solving Problems with Constraints: Many real-world problems involve constraints that are best expressed as inequalities. For example, a budget might require total spending to be less than a certain amount, or the capacity of a vehicle might dictate that the load must be less than a specific weight. Solving these inequalities helps determine feasible solutions.
- Graphing Inequalities on a Number Line: Less than inequalities can be visually represented on a number line. Typically, an open circle is used at the boundary value (e.g., at '10' for x < 10) to denote that the boundary value is not included in the solution set, with a line extending to the left to show all values smaller than it. Understanding the crucial difference between "less than" (<) and "less than or equal to" (≤) is paramount here, as the latter includes the boundary value, usually represented by a closed circle, signifying that the boundary itself is part of the solution.
- Boolean Logic and Programming: The less than symbol is also used as a boolean operator in computer science and logic, returning true or false based on the comparison. This fundamental notation simplifies comparisons and expresses relationships between numerical values efficiently, forming the backbone of conditional statements and control flow in programming languages. For instance, an `if` statement like `if (score < 60)` would execute a block of code only if the `score` variable holds a value strictly less than 60.
The ability to work with these inequalities is a foundational skill for advanced mathematics, critical thinking, and problem-solving in numerous professional and academic disciplines. Learning the meaning and usage of the inequalities symbols >, ≥, ≤, ≠, and how to remember them is essential for mathematical fluency.
Teaching and Remembering the Less Than Sign: Tricks and Tips
One of the common struggles for students (and even adults refreshing their knowledge) is remembering which symbol is which: is it < or > for "less than"? This confusion is natural, given the similar appearance of the two primary inequality signs. Fortunately, several memorable tricks and methods have been developed to make this distinction intuitive and permanent. These methods leverage visual cues and relatable analogies to solidify understanding of the less than sign and its counterparts.
The Alligator Method
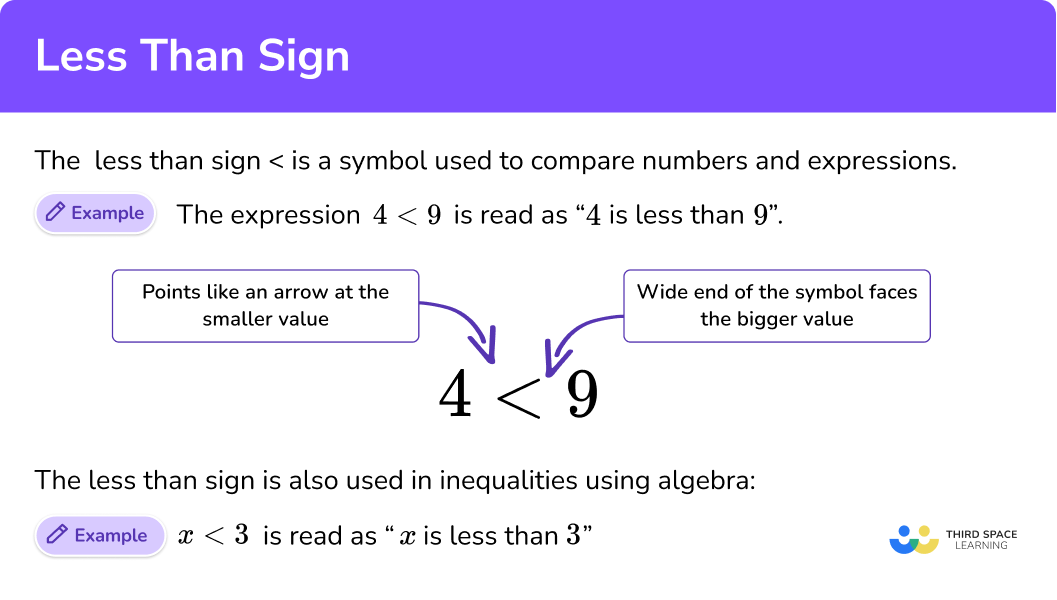
Perhaps the most popular and effective mnemonic for remembering inequality signs is the "alligator method" or "crocodile method." This trick personifies the inequality symbol as an alligator's mouth, which always wants to eat the larger number. The wide open side of the symbol faces the larger number, just as an alligator's mouth would open wide to consume the biggest meal. Conversely, the pointed, closed end of the symbol always points to the smaller number. This method is universally recognized and widely used in elementary education to teach comparison symbols.
For example, to show "6 is less than 8," you would write "6 < 8." Here, the alligator's mouth (the open side) is facing the '8' (the larger number), and the pointed end is pointing to the '6' (the smaller number). Similarly, for "10 is greater than 5," you would write "10 > 5," with the alligator's mouth open towards the '10'. This vivid imagery makes it incredibly easy to recall the correct orientation of the less than sign and its counterpart, the greater than sign. It transforms an abstract symbol into a relatable, memorable character.
The 'L' Method and Other Visual Cues
Another simple yet highly effective trick for remembering the less than sign specifically is the "L" method. If you draw the less than symbol (<) and then slightly extend the top left line downwards, it forms a crude letter 'L'. This 'L' stands for "Less Than." This visual mnemonic works exclusively for the less than sign, providing a quick mental check when you're unsure. It's a simple, direct association that many find incredibly helpful.
Other visual cues and memory aids include:
- The Small End Always Points to the Smaller Number: This is a universal rule for both < and >. The narrow, pointed end of the symbol always points towards the smaller value. So, for "6 < 8," the pointed end points to '6'. This consistent rule provides a reliable way to orient the symbol regardless of which side the smaller number is on.
- The Open End Faces the Larger Number: Conversely, the wide, open end of the symbol always faces the
Less Than Sign - GCSE Maths - Steps, Examples & Worksheet
Less Than Symbol ( ≤<≮ ) Copy and Paste Text Symbols
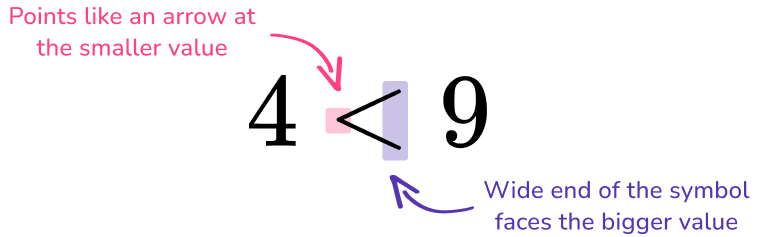
Less Than Sign - Math Steps, Examples & Questions